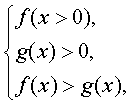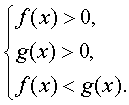细å“æ•™æ
一ã€å¯¹æ•°å‡½æ•°
1.概念:一般地,我们把函数y=logax(a>0,且a≠1)å«åšå¯¹æ•°å‡½æ•°ï¼Œå…¶ä¸x是自å˜é‡ï¼Œy是x的函数.
2.定义域ã€å€¼åŸŸï¼šå¯¹æ•°å‡½æ•°çš„定义域是(0,+∞),值域是实数集R.
技术æ示
一个函数为对数函数的æ¡ä»¶æ˜¯ï¼š(1)系数为1ï¼›(2)底数为大于0且ä¸ç‰äºŽ1çš„æ£å¸¸æ•°ï¼›(3)自å˜é‡ä¸ºæ£æ•°ï¼Œå³åªæœ‰å½¢å¦‚y=logax(a>0,a≠1,x>0)的函数æ‰å«åšå¯¹æ•°å‡½æ•°.åƒy=loga(x+1),y=2logax,y=logax+3ç‰å‡½æ•°ï¼Œå®ƒä»¬æ˜¯ç”±å¯¹æ•°å‡½æ•°å˜åŒ–而得到的,都ä¸æ˜¯å¯¹æ•°å‡½æ•°ï¼Œè€Œæ˜¯ä¸€äº›å¤åˆå‡½æ•°ï¼Œæˆ‘们å¯ä»¥ç§°å…¶ä¸ºå¯¹æ•°åž‹å‡½æ•°.对数函数åŒæŒ‡æ•°å‡½æ•°ä¸€æ ·éƒ½æ˜¯åŸºæœ¬åˆç‰å‡½æ•°.
ã€ç¤ºä¾‹ã€‘求下列函数的定义域.
(1)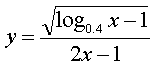 ï¼›(2)
ï¼›(2)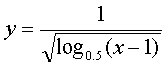 .
.
æ€è·¯åˆ†æžï¼šå®šä¹‰åŸŸæ˜¯ä½¿è§£æžå¼æœ‰æ„义的自å˜é‡çš„å–值范围,对数函数的定义域的求解è¦æ³¨æ„对数的性质.
解:(1)è¦ä½¿å‡½æ•°æœ‰æ„义,必须且åªéœ€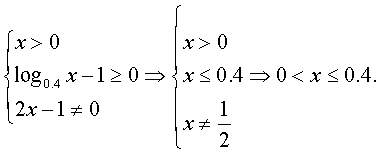
∴函数的定义域为(0,0.4].
(2)è¦ä½¿å‡½æ•°æœ‰æ„义,必须且åªéœ€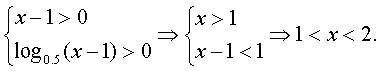
∴函数的定义域为(1,2).
二ã€å¯¹æ•°å‡½æ•°çš„图象和性质
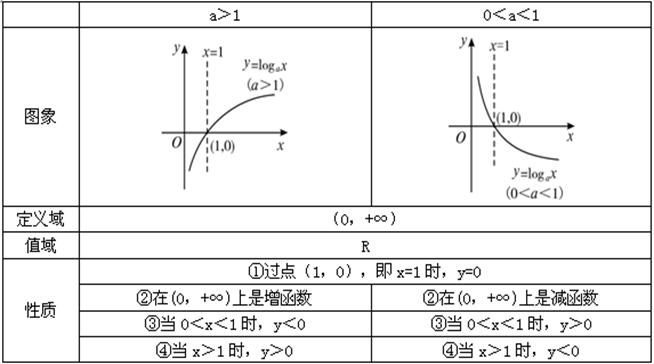
对数函数y=logax在底数a>1åŠ0<a<1这两ç§æƒ…况下的图象和性质如下表所示:
技术æ示
(1)对数函数的图象æ’在yè½´å³æ–¹ï¼Œå…¶å•è°ƒæ€§å–决于底数;
(2)设y1=logax,y2=logbx,其ä¸a>1,b>1或0<a<1,0<b<1.在x轴上方,当x>1时,底大图低,å³è‹¥a>b,则y1<y2;当0<x<1时,底大图高,å³è‹¥a>b,则y1>y2.
ã€ç¤ºä¾‹ã€‘图2.2.2-1ä¸æ›²çº¿æ˜¯å¯¹æ•°å‡½æ•°y=logax的图象,已知a值å– ,
,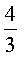 ,
,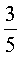 ,
,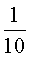 ,则相应于C1,C2,C3,C4çš„a值ä¾æ¬¡ä¸ºï¼ˆ )
,则相应于C1,C2,C3,C4çš„a值ä¾æ¬¡ä¸ºï¼ˆ )
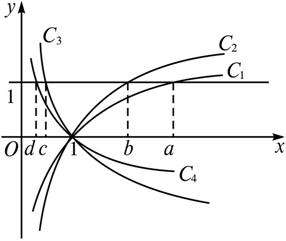
图2.2.2-1
A.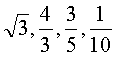
B.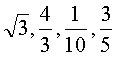
C.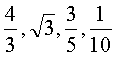
D.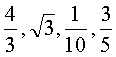
æ€è·¯åˆ†æžï¼šå› 为对数的底数越大,函数图象越远离yè½´çš„æ£æ–¹å‘,所以C1,C2,C3,C4çš„a值ä¾æ¬¡ç”±å¤§åˆ°å°ï¼Œå³C1,C2,C3,C4çš„a值ä¾æ¬¡ä¸º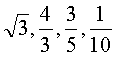 .
.
å¦å¤–过点(0,1)作平行于x轴的直线,与C1,C2,C3,C4的交点的横åæ ‡ï¼Œå³ä¸ºå„对数底的值.
ç”案:A
三ã€å¯¹æ•°å‡½æ•°çš„å函数
1.对数函数的å函数:指数函数y=ax(a>0且a≠1)与对数函数y=logax(a>0,且a≠1)互为å函数.
2.互为å函数的有关性质:(1)原函数的定义域ã€å€¼åŸŸæ°å¥½æ˜¯å函数的值域ã€å®šä¹‰åŸŸï¼›(2)互为å函数的两个函数的图象关于直线y=x对称.
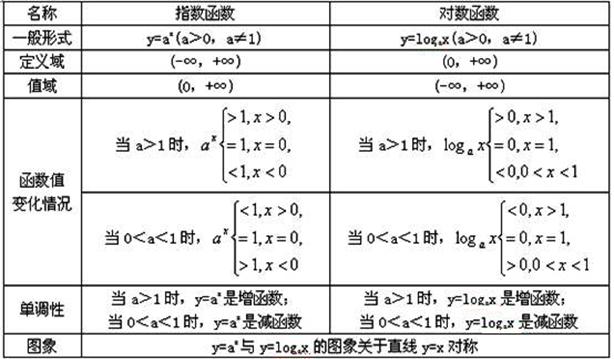
3.指数函数与对数函数特å¾å¯¹æ¯”:
由于指数函数与对数函数互为å函数,所以它们的许多特å¾éƒ½æ˜¯ç›¸ä¼¼çš„,现将它们列表对比如下:
技术æ示
通常当一个函数在定义域内å•è°ƒæ—¶ï¼Œå¯ç”±ä¸‹é¢çš„æ¥éª¤æ±‚出其å函数:
(1)ç”±y=f(x)解出xï¼›(2)把x替æ¢ä¸ºy,y替æ¢ä¸ºx,得å函数解æžå¼ï¼›(3)写出解æžå¼çš„定义域(å³ä¸ºåŽŸå‡½æ•°çš„值域).
状元笔记
并ä¸æ˜¯æ¯ä¸ªå‡½æ•°éƒ½æœ‰å函数,有些函数没有å函数,如y=x2.一般æ¥è¯´ï¼Œå•è°ƒå‡½æ•°æœ‰å函数.
ã€ç¤ºä¾‹ã€‘求函数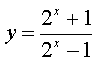 çš„å函数.
çš„å函数.
æ€è·¯åˆ†æžï¼šè¦æ±‚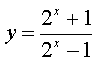 çš„å函数,需从
çš„å函数,需从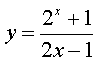 ä¸æ±‚出x,得
ä¸æ±‚出x,得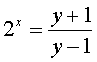 .å› 2x>0,则
.å› 2x>0,则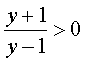 ,求得原函数的值域å³å函数的定义域.把指数å¼åŒ–æˆå¯¹æ•°å¼å¯å¾—å函数.
,求得原函数的值域å³å函数的定义域.把指数å¼åŒ–æˆå¯¹æ•°å¼å¯å¾—å函数.
解:由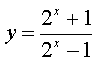 ,得2x(y-1)=y+1.â‘
,得2x(y-1)=y+1.â‘
∵y≠1,∴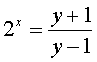 .∵2x>0,∴
.∵2x>0,∴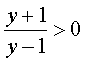 ,解得y>1,或y<-1.
,解得y>1,或y<-1.
æ•…å函数的定义域是{x|x>1或x<-1}.
由①å¼ï¼Œå¾—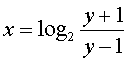 .
.
所求的å函数为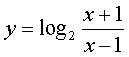 (x<-1或x>1).
(x<-1或x>1).
归纳整ç†
本节的主è¦å†…容是对数函数的概念ã€å›¾è±¡å’Œæ€§è´¨åŠå…¶å函数.é‡ç‚¹æ˜¯ç†è§£å¯¹æ•°å‡½æ•°åŠå…¶å函数的关系,掌æ¡å¯¹æ•°å‡½æ•°çš„å›¾è±¡å’Œæ€§è´¨ï¼Œå¹¶èƒ½æ ¹æ®å›¾è±¡ã€æ€§è´¨è§£å†³ç›¸å…³é—®é¢˜ï¼Œç‰¹åˆ«æ˜¯å…¶å•è°ƒæ€§çš„应用,是解决问题的关键点.

ç”案:①y=logax(a>0,且a≠1) â‘¡(0,+∞) ③增 â‘£å‡ â‘¤æŒ‡æ•°å‡½æ•°y=ax(a>0,且a≠1) â‘¥y=x
综åˆæŽ¢ç©¶
1.对数函数值的å˜åŒ–规律
在åŒä¸€åæ ‡ç³»ä¸ï¼Œç”»å‡ºy=log3x,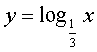 ,y=log2x,
,y=log2x,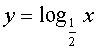 的图象如图2.2.2-2.从图ä¸å¯ä»¥çœ‹åˆ°ï¼šæ‰€æœ‰å›¾è±¡éƒ½è·¨è¶Šç¬¬ä¸€ã€å››è±¡é™ï¼Œä»»ä½•ä¸¤ä¸ªå›¾è±¡éƒ½æ˜¯äº¤å‰å‡ºçŽ°çš„,交å‰ç‚¹æ˜¯(1,0).当a>1时,图象å‘下与yè½´çš„è´ŸåŠè½´æ— é™é 拢,在点(1,0)çš„å³ä¾§ï¼Œå‡½æ•°å€¼æ’大于0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越å°ï¼Œåœ¨ç‚¹(1,0)的左侧,函数值æ’å°äºŽ0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越大;当0<a<1时,图象å‘上与yè½´çš„æ£åŠè½´æ— é™é 拢,在点(1,0)的左侧,函数值æ’大于0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越大,在点(1,0)çš„å³ä¾§ï¼Œå‡½æ•°å€¼æ’å°äºŽ0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越å°.
的图象如图2.2.2-2.从图ä¸å¯ä»¥çœ‹åˆ°ï¼šæ‰€æœ‰å›¾è±¡éƒ½è·¨è¶Šç¬¬ä¸€ã€å››è±¡é™ï¼Œä»»ä½•ä¸¤ä¸ªå›¾è±¡éƒ½æ˜¯äº¤å‰å‡ºçŽ°çš„,交å‰ç‚¹æ˜¯(1,0).当a>1时,图象å‘下与yè½´çš„è´ŸåŠè½´æ— é™é 拢,在点(1,0)çš„å³ä¾§ï¼Œå‡½æ•°å€¼æ’大于0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越å°ï¼Œåœ¨ç‚¹(1,0)的左侧,函数值æ’å°äºŽ0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越大;当0<a<1时,图象å‘上与yè½´çš„æ£åŠè½´æ— é™é 拢,在点(1,0)的左侧,函数值æ’大于0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越大,在点(1,0)çš„å³ä¾§ï¼Œå‡½æ•°å€¼æ’å°äºŽ0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越å°.
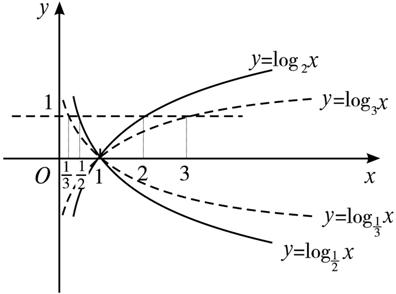
图2.2.2-2
我们知é“,对于对数函数y=logax,当y=1时,x=a,而aæ°å¥½æ˜¯å¯¹æ•°å‡½æ•°çš„底数,这就å¯å‘我们,ä¸å¦¨ä½œç›´çº¿y=1,它åŒå„个图象相交,交点的横åæ ‡æ°å¥½å°±æ˜¯å¯¹æ•°å‡½æ•°çš„底数,以æ¤å¯æ¯”较底数的大å°.åŒæ—¶ï¼Œæ ¹æ®ä¸åŒå›¾è±¡é—´çš„关系,也å¯æ¯”较真数相åŒï¼Œåº•æ•°ä¸åŒçš„对数函数值的大å°ï¼Œå¦‚log23<log1.53,log20.5<log30.5,log0.52>log0.62ç‰.
2.如何比较对数的大å°
利用其性质å¯ä»¥æ¯”较两对数å¼çš„大å°ï¼Œå¸¸ç”¨çš„方法是:当底数相åŒçœŸæ•°ä¸ç›¸åŒæ—¶ï¼Œç›´æŽ¥åˆ©ç”¨å¯¹æ•°å‡½æ•°çš„å•è°ƒæ€§è¿›è¡Œæ¯”较,å³a>1时,在(0,+∞)上是增函数,0<a<1时,在(0,+∞)上是å‡å‡½æ•°ï¼›
当底数ä¸ç›¸åŒï¼ŒçœŸæ•°ç›¸åŒæ—¶ï¼Œå¯æ ¹æ®å›¾è±¡ä¸Žåº•æ•°çš„关系所åæ˜ å‡ºçš„è§„å¾‹è¿›è¡Œæ¯”è¾ƒï¼Œå½“åº•æ•°å’ŒçœŸæ•°å„ä¸ç›¸åŒæ—¶ï¼Œå¯è€ƒè™‘引进第三个数(常用“0â€æˆ–“1â€)åˆ†åˆ«ä¸Žä¹‹æ¯”è¾ƒï¼Œé€šè¿‡ç¬¬ä¸‰ä¸ªæ•°çš„ä¼ é€’è¿›è€Œæ¯”è¾ƒå‡ºä¸¤æ•°çš„å¤§å°.当底数与1的大å°å…³ç³»æœªæ˜Žç¡®æŒ‡å®šæ—¶ï¼Œè¦åˆ†æƒ…况对底数进行讨论æ¥æ¯”较两个对数的大å°.
对于多个数的大å°æ¯”较,通常先找出(-∞,0)ã€(0,1)ã€(1,+∞)ä¸çš„å„数,然åŽæŠŠä½äºŽåŒä¸€åŒºé—´ä¸çš„æ•°å†è¿›è¡Œæ¯”较.
3.å函数的拓展
定义:设Aã€B分别为函数y=f(x)的定义域和值域,如果由函数y=f(x)所解得的x=φ(y)也是一个函数(å³å¯¹ä»»æ„的一个y∈B都有唯一的x∈A与之对应).那么就称x=φ(y)是函数y=f(x)çš„å函数;记作x=f-1(y),在x=f-1(y)ä¸ï¼Œy是自å˜é‡ï¼Œx是yçš„å‡½æ•°ï¼Œä½†åœ¨ä¹ æƒ¯ä¸ŠæŠŠä¸Šå¼æ”¹å†™æˆy=f-1(x)(x∈B,y∈A)çš„å½¢å¼.
如求函数y=3x+6(x∈R)çš„å函数,从y=3x+6ä¸è§£å‡º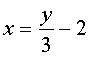 (y∈R)ï¼Œè¿™æ ·å‡½æ•°y=3x+6(x∈R)çš„å函数为
(y∈R)ï¼Œè¿™æ ·å‡½æ•°y=3x+6(x∈R)çš„å函数为 (x∈R).
(x∈R).
由定义å¯ä»¥çœ‹å‡ºï¼Œå‡½æ•°y=f(x)的定义域Aæ£å¥½æ˜¯å®ƒçš„å函数y=f-1(x)的值域;函数y=f(x)的值域Bæ£å¥½æ˜¯å®ƒçš„å函数y=f-1(x)的定义域.
判æ–一个函数是å¦å˜åœ¨å函数å¯ä»Žä»¥ä¸‹ä¸¤ç‚¹è¿›è¡Œï¼š
(1)从函数观点æ¥çœ‹ï¼Œå°±æ˜¯ç”±å¼åy=f(x)解出x,得x=φ(y)åŽï¼Œçœ‹å¯¹äºŽå€¼åŸŸå†…ä»»æ„一个y的值,由å¼åx=φ(y)是å¦èƒ½ç¡®å®šå®šä¹‰åŸŸå†…有唯一的x值与之对应.
(2)用图象æ¥åˆ¤æ–,就是看函数y=f(x)的图象与任æ„一垂直于y轴的直线是å¦è‡³å¤šåªæœ‰ä¸€ä¸ªäº¤ç‚¹.
æ ¹æ®ä»¥ä¸Šä¸¤ç‚¹ï¼Œæˆ‘们å¯ä»¥å¾—到两个éžå¸¸æœ‰ç”¨çš„结论,å³ï¼šâ‘ å•è°ƒå‡½æ•°å¿…有å函数;②图象关于y轴对称的函数ä¸å˜åœ¨å函数.
æ€è€ƒå‘现
1.求函数定义域时,常è§çš„é™åˆ¶æ¡ä»¶æœ‰ï¼šåˆ†æ¯ä¸ä¸ºé›¶ï¼Œå¼€å¶æ¬¡æ–¹æ—¶è¢«å¼€æ–¹æ•°éžè´Ÿï¼Œå¯¹æ•°çš„真数大于零,底数大于零且ä¸ç‰äºŽ1ç‰.
2.对数函数y=logax(a>0,a≠1)的图象,å¯æ ¹æ®å®ƒä¸ŽæŒ‡æ•°å‡½æ•°y=ax(a>0,a≠1)的图象关于直线y=x对称æ¥ç”»ï¼Œå³ç”¨æ‰¾å¯¹ç§°ç‚¹ä½œå¯¹ç§°å›¾å½¢çš„方法.也å¯ä»¥ç”¨åˆ—表ã€æ点ã€è¿žçº¿çš„方法æ¥ç”».首先è¦åˆ†æ¸…底数a>1还是0<a<1,明确图象的走å‘,然åŽè‡³å°‘è¦ç”»å‡ºä¸‰ä¸ªå…³é”®ç‚¹ï¼š(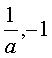 ),(1,0),(a,1),最åŽè¿žçº¿.当然画出的点越多,所画图象越准确.
),(1,0),(a,1),最åŽè¿žçº¿.当然画出的点越多,所画图象越准确.
3.利用对数的å•è°ƒæ€§å¯è§£ç®€å•çš„对数ä¸ç‰å¼.解对数ä¸ç‰å¼çš„关键是把真数视为一个整体,用对数函数的å•è°ƒæ€§æž„é€ ä¸ç‰å¼ï¼Œä½†ä¸€å®šè¦æ³¨æ„真数大于零这一éšå«æ¡ä»¶.
若logaf(x)>logag(x),则当a>1时,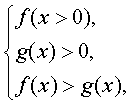
当0<a<1时,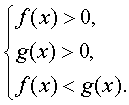
4.比较两个数或å¼å的大å°æ—¶ï¼Œå¸¸ç”¨çš„方法是作差法.用作差法比较大å°æ—¶ï¼Œè‹¥æ•°æˆ–å¼åå«æœ‰ç»å¯¹å€¼æ—¶éœ€å…ˆåŽ»æŽ‰ç»å¯¹å€¼ç¬¦å·.ç”¨å‡½æ•°çš„è§‚ç‚¹ç ”ç©¶æ–¹ç¨‹é—®é¢˜æ—¶ï¼Œæ–¹ç¨‹è§£çš„ä¸ªæ•°å°±æ˜¯ä¸¤ä¸ªå‡½æ•°å›¾è±¡äº¤ç‚¹çš„ä¸ªæ•°ï¼Œæ–¹ç¨‹çš„è§£å°±æ˜¯ä¸¤ä¸ªå‡½æ•°å›¾è±¡äº¤ç‚¹çš„æ¨ªåæ ‡.
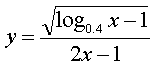 ï¼›(2)
ï¼›(2)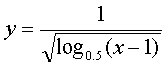 .
.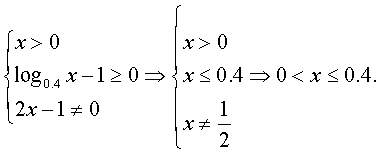
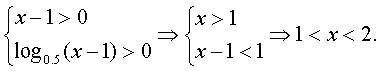

 ,
,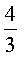 ,
,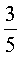 ,
,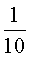 ,则相应于C1,C2,C3,C4çš„a值ä¾æ¬¡ä¸ºï¼ˆ )
,则相应于C1,C2,C3,C4çš„a值ä¾æ¬¡ä¸ºï¼ˆ )
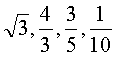
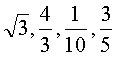
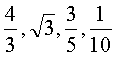
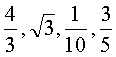
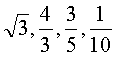 .
.
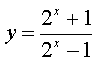 çš„å函数.
çš„å函数.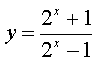 çš„å函数,需从
çš„å函数,需从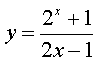 ä¸æ±‚出x,得
ä¸æ±‚出x,得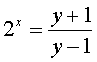 .å› 2x>0,则
.å› 2x>0,则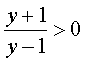 ,求得原函数的值域å³å函数的定义域.把指数å¼åŒ–æˆå¯¹æ•°å¼å¯å¾—å函数.
,求得原函数的值域å³å函数的定义域.把指数å¼åŒ–æˆå¯¹æ•°å¼å¯å¾—å函数.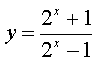 ,得2x(y-1)=y+1.â‘
,得2x(y-1)=y+1.①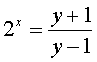 .∵2x>0,∴
.∵2x>0,∴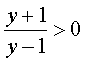 ,解得y>1,或y<-1.
,解得y>1,或y<-1.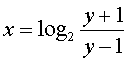 .
.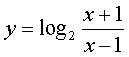 (x<-1或x>1).
(x<-1或x>1).
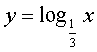 ,y=log2x,
,y=log2x,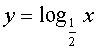 的图象如图2.2.2-2.从图ä¸å¯ä»¥çœ‹åˆ°ï¼šæ‰€æœ‰å›¾è±¡éƒ½è·¨è¶Šç¬¬ä¸€ã€å››è±¡é™ï¼Œä»»ä½•ä¸¤ä¸ªå›¾è±¡éƒ½æ˜¯äº¤å‰å‡ºçŽ°çš„,交å‰ç‚¹æ˜¯(1,0).当a>1时,图象å‘下与yè½´çš„è´ŸåŠè½´æ— é™é 拢,在点(1,0)çš„å³ä¾§ï¼Œå‡½æ•°å€¼æ’大于0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越å°ï¼Œåœ¨ç‚¹(1,0)的左侧,函数值æ’å°äºŽ0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越大;当0<a<1时,图象å‘上与yè½´çš„æ£åŠè½´æ— é™é 拢,在点(1,0)的左侧,函数值æ’大于0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越大,在点(1,0)çš„å³ä¾§ï¼Œå‡½æ•°å€¼æ’å°äºŽ0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越å°.
的图象如图2.2.2-2.从图ä¸å¯ä»¥çœ‹åˆ°ï¼šæ‰€æœ‰å›¾è±¡éƒ½è·¨è¶Šç¬¬ä¸€ã€å››è±¡é™ï¼Œä»»ä½•ä¸¤ä¸ªå›¾è±¡éƒ½æ˜¯äº¤å‰å‡ºçŽ°çš„,交å‰ç‚¹æ˜¯(1,0).当a>1时,图象å‘下与yè½´çš„è´ŸåŠè½´æ— é™é 拢,在点(1,0)çš„å³ä¾§ï¼Œå‡½æ•°å€¼æ’大于0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越å°ï¼Œåœ¨ç‚¹(1,0)的左侧,函数值æ’å°äºŽ0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越大;当0<a<1时,图象å‘上与yè½´çš„æ£åŠè½´æ— é™é 拢,在点(1,0)的左侧,函数值æ’大于0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越大,在点(1,0)çš„å³ä¾§ï¼Œå‡½æ•°å€¼æ’å°äºŽ0,对åŒä¸€è‡ªå˜é‡x而言,底数越大,函数值越å°.
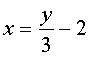 (y∈R)ï¼Œè¿™æ ·å‡½æ•°y=3x+6(x∈R)çš„å函数为
(y∈R)ï¼Œè¿™æ ·å‡½æ•°y=3x+6(x∈R)çš„å函数为 (x∈R).
(x∈R).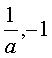 ),(1,0),(a,1),最åŽè¿žçº¿.当然画出的点越多,所画图象越准确.
),(1,0),(a,1),最åŽè¿žçº¿.当然画出的点越多,所画图象越准确.