经典例题
基础知识题型
一、已知受力求运动
例1:一个滑雪人从静止开始沿山坡滑下,山坡的倾角θ=30°,滑雪板与雪地的动摩擦因数是0.04,求5 s内滑下来的路程和5 s末的速度大小.
{@ts}根据受力求得加速度,再用运动学公式求速度.{@/ts}
{@jx}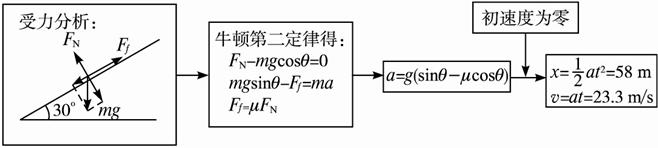
以滑雪人为研究对象,受力情况如图所示.
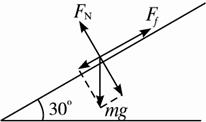
研究对象的运动状态为:垂直于山坡方向,处于平衡;沿山坡方向,做匀加速直线运动.
将重力mg分解为垂直于山坡方向和沿山坡方向的力,据牛顿第二定律列方程:
FN-mgcosθ=0①
mgsinθ-Ff=ma②
又因为Ff=μFN③
由①②③可得a=g(sinθ-μcosθ),
故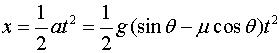
 ,
,
 .{@/jx}
.{@/jx}
{@da}58 m 23.3 m/s
技术点拨:这是一个典型的已知物体的受力情况求物体的运动情况的问题,解决此类问题的基本思路是:根据受力分析→定合外力据 确定加速度a
确定加速度a 确定运动情况.{@/da}
确定运动情况.{@/da}
二、已知运动求受力
例2:一位滑雪者如果以v0=20 m/s的初速度沿直线冲上一倾角为30°的山坡,从冲坡开始计时,至3.8 s末,雪橇速度变为零,如果雪橇与人的质量为m=80 kg,求滑雪人受到的阻力是多少.(g取10 m/s2)
{@ts}根据运动学公式求得加速度,再由牛顿第二定律求出力的大小.{@/ts}
{@jx} {@/jx}
{@/jx}
{@da}20.8 N
技术点拨:先由运动学方程求出加速度,再根据受力情况求对应的外力,并且在此类问题中正交分解法运用得相当普遍.{@/da}
综合拓展题型
三、连接体
例3:两个物体A和B,质量分别为m1和m2,互相接触放在光滑水平面上,如图所示,对物体A施以水平的推力F,则物体A对物体B的作用力等于( )
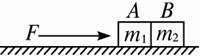
A.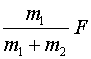
B. 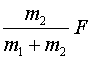
C.F
D.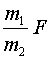
{@ts}隔离法和整体法综合运用.{@/ts}
{@jx}
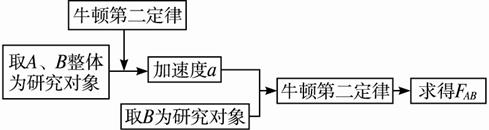
对A、B整体分析,则F=(m1+m2)a
所以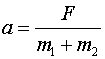
求A、B间的弹力FN时以B为对象,则
 .{@/jx}
.{@/jx}
{@da}B
技术点拨:当连接体的各个部分加速度相同时,既可以整体为研究对象,利用牛顿第二定律列方程,也可以隔离各个部分,利用牛顿第二定律列方程.如果连接体的各个部分的加速度不同,则只能隔离各个部分,利用牛顿第二定律列方程求解.{@/da}
四、临界条件
例4:如图所示,一细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处,细线的另一端拴一质量为m的小球.试求当滑块以a=2g的加速度向左运动时线中的拉力FT.
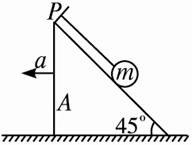
{@ts}首先求出小球即将离开斜面时的加速度.{@/ts}
{@jx} {@/jx}
{@/jx}
{@da}当滑块向左运动的加速度为某一临界值时,斜面对小球的支持力恰好为零(小球将要离开斜面而“飘”起来).我们首先求此临界条件,此时小球受两个力:重力mg;绳的拉力FT.根据牛顿第二定律的正交表示,有
FT·cosθ=ma①
FT·sinθ-mg=0②
联立①②两式并将θ=45°代入,得
a=g,
即当斜面体滑块向左运动的加速度为a=g时,小球恰好对斜面无压力.
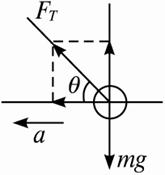
当a>g时,小球将“飘”起来,当a=2g时,小球已“飘”起来了,此时小球的受力情况正如图所示,故根据①②两式并将a=2g代入,解得
 .
.
此即为所求线中的拉力.
技术点拨:在本题的解析过程中,通过对临界条件的求解,可清楚看到,当a>g时,绳与水平方向的夹角小于45°,且a越大,夹角θ越小(其极限值为:a→∞时,θ→0).很多同学在求解此题时常犯下列错误:由方程①得FT·cos45°=m·2g,从而得FT=22·mg.实际上a=2g时球已离开斜面,线与水平方向的夹角不是45°了.{@/da}
探究创新题型
例5:放在水平地面上的一物块,受到方向不变的水平推力F的作用,F的大小与时间t的关系和物块速度v与时间的关系如图所示,取重力加速度g=10m/s2.试利用两图线求出物块的质量及物块与地面间的动摩擦因数.
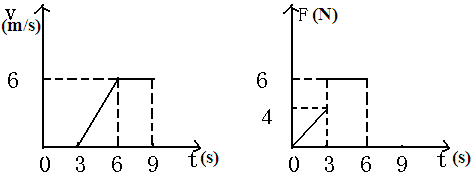
{@ts}充分挖掘图象中所给信息.{@/ts}
{@jx}由v-t图象可知,物块在0~3 s内静止,3 s~6 s内做匀加速运动,加速度为a,6 s~9 s内做匀速运动,结合F-t图形可知.
Ff=4 N=μmg,
F3-F2=2 N=ma,
v2=6 m/s=at=a×3
由以上各式得m=1 kg,μ=0.4.{@/jx}
{@da}1 kg 0.4
技术点拨:本例的已知条件是通过图象给出的.由F-t图象知力F为变力,相应物体速度在三段时间内变化的快慢不同,即加速度不同.根据牛顿第二定律的同一性和瞬时性,各阶段的受力决定相应阶段的加速度,这是解决问题的关键.{@/da}

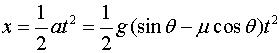
 ,
, .{@/jx}
.{@/jx} 确定加速度a
确定加速度a 确定运动情况.{@/da}
确定运动情况.{@/da} {@/jx}
{@/jx}
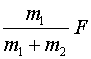
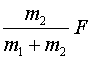
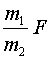

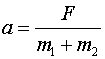
 .{@/jx}
.{@/jx}
 {@/jx}
{@/jx}
 .
.