学习理解
一､切线的定义､判定与性质
1.切线的定义:和圆只有一个公共点的直线叫做圆的切线,这个公共点叫做切点.
2.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
3.判定一条直线是不是圆的切线,除运用切线的判定定理外,还有下面两种判定方法:
(1)切线的定义;
(2)和圆心的距离等于圆的半径的直线是圆的切线.
4.切线的性质定理:圆的切线垂直于过切点的半径.
5.由切线的性质定理可得两条推论:
(1)经过圆心且垂直于切线的直线必过切点;
(2)经过切点且垂直于切线的直线必过圆心.
6.切线的性质定理与推论综合起来说明:如果一条直线满足下列三个条件中的任何两条,那么就一定可以得出第三条,三个条件是①垂直于切线;②经过切点;③经过圆心.
7.弦切角：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。
8.弦切角定理：弦切角等于它所夹的弧所对的圆周角。 弦切角等于它所夹的弧所对的圆心角的一半。
两个弦切角所夹的弧相等，那么这两个弦切角也相等。
【示例】如图,已知OC平分∠AOB,D是OC上一点,⊙D与OA相切于点E.求证:OB与⊙D相切.

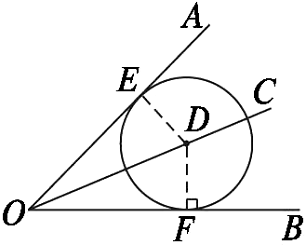
分析:要证OB与⊙D相切,根据切线的判定,需证OB经过⊙D的半径外端,且垂直于这条半径.这由⊙D与OA相切于点E和OC平分∠AOB可证.
证明:连接DE,作DF⊥OB于F.
∵⊙D与OA相切于点E,
∴DE⊥OA.
∵OC平分∠AOB,
∴DF=DE,
∴OB与⊙D相切.
二､切线长
1.切线长定义:一般把圆的切线上某一点与切点之间的线段的长,叫做这点到圆的切线长.
2.切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这点和圆心的连线平分这两条切线的夹角.
3.利用切线长定理证明相关线段相等､角相等和线与线的垂直关系,通常连接切点和圆心构造直角三角形解决问题.
4.切线和切线长是两个完全不同的概念,必须弄清楚.切线是直线,是不能度量的;切线长是一条线段的长,这条线段的两个端点一个是圆外一点,另一个是切点.
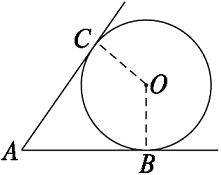
【示例】如图,AB､AC与⊙O相切于B､C,∠A=50°,P是圆上不与B､C重合的点,则∠BPC的度数是(  ).

A.65°
B.115°
C.65°或115°
D.130°或150°
分析:若点P在优弧上,连接OB､OC,则有∠BOC=130°.
所以∠BPC=∠BOC=65°.若点P在劣弧上,同理可求得∠BPC=115°.
答案:C
三､三角形的内切圆和内心
1.和三角形各边都相切的圆叫做三角形的内切圆,这个三角形又叫圆的外切三角形.三角形内切圆的圆心叫做三角形的内心.
2.一个三角形有且只有一个内切圆,而一个圆却有无数个外切三角形.
3.由三角形的内心可知:锐角三角形､直角三角形和钝角三角形的内心都在三角形的内部.
4.三角形内切圆的作法:
如图,①分别作∠B､∠C的平分线BE､CF,设交点为I;
②过I作ID⊥BC于点D;
③以I为圆心,ID为半径作⊙I,则⊙I就是所求作的圆.

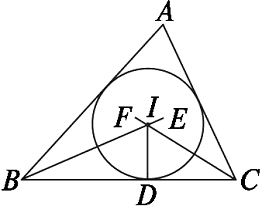
三角形的内心是三角形三条角平分线的交点,所以当三角形的内心已知时,过三角形的顶点和内心的射线,必平分三角形的内角.因此,可利用它证明相关角相等.
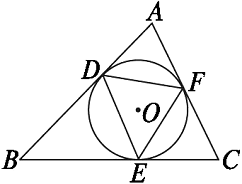
【示例】如图,已知△ABC的内切圆O与各边相切于点D､E､F,那么点O是△DEF的(  ).

A.外心
B.内心
C.重心
D.垂心
分析:因为点O是△ABC的内切圆的圆心,内切圆O与各边相切于点D､E､F,由三角形内心的定义,可知OD=OE=OF,所以点O是△DEF的外心.
答案:A