典例精析
题型一　投影问题
【例1】下列命题中正确的个数是(　　)
①直线或线段的平行投影仍是直线或线段
②与投射面平行的平面图形,它的投影与这个图形一定全等
③矩形的平行投影一定是矩形
④两条相交直线的投影可能平行
⑤如果△ABC在一投射面内的平行投影是△A′B′C′,则△ABC的重心M在投射面内的平行投影M′一定是△A′B′C′的重心
A.1  
B.2   
C.3  
D.4
{@ts}①当直线垂直投射面时,其平行投影为点，错误,故①错误；②正确;③错误,如矩形的窗子被阳光投射在地面上的投影图形就可能为一个平行四边形;④错误,两条相交直线的投影可能是相交直线或重合的直线,不可能平行;⑤正确,重心的平行投影仍是重心.{@/ts}
{@jx}{@/jx}
{@da}B
技术感悟：领会好平行投影的定义,由于立体几何画图总是用平行投影,所以平行投影也常简称为投影.{@/da}

题型二　用中心投影解决实际问题
【例2】某天,小明站在室内,室内有一面积为3平方米的玻璃窗,他站在离窗子4米的地方向外看,他能看到窗前面一幢楼的面积有多大?(楼层之间的距离为20米)
{@ts}由眼睛向外看的视线,可以看作是中心投影,所求的面积可用相似比求解.{@/ts}
{@jx}

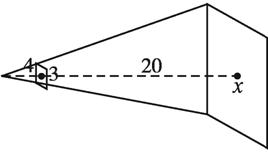
图1.2.2-9{@/jx}
{@da}设看到的面积为x m²,根据视线是直线,窗子和小明看到的前面一幢楼的平面图形是相似的,所以有,解得x=108,即小明能看到窗外前一幢楼的面积约为108平方米.
技术感悟：本题的实际模型是一个中心投影问题.对于此类题目,经常要把它转化到平面图形的相似形来解决.{@/da}

题型三　三视图的布局及画法
【例3】画出如图1.2.2-10所示物体的三视图.

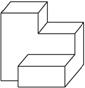
图1.2.2-10
{@ts}正面观察的方向为正视图的方向,把看见的棱画成实线,画好正视图和俯视图后再画出侧视图,想象视图中看不见的棱用虚线画出.{@/ts}
{@jx}{@/jx}
{@da}这个几何体的三视图如图1.2.2-11所示.

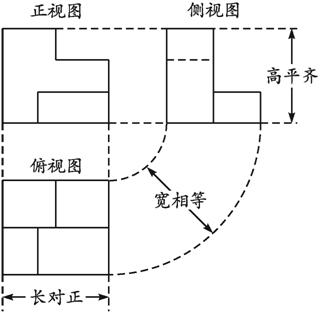
图1.2.2-11
技术感悟：画三视图应注意:
(1)俯视图在正视图的下面,侧视图在正视图的右边.
(2)画法规则:“长对正,高平齐,宽相等”或“正侧一样高,正俯一样长,俯侧一样宽”.
(3)观察时看不见的棱用虚线画出.{@/da}

题型四　组合体的三视图
【例4】螺栓是棱柱和圆柱构成的组合体,如图1.2.2-12,画出它的三视图.

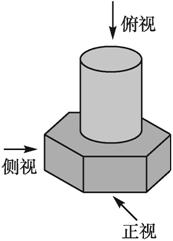
图1.2.2-12
{@ts}螺栓是六棱柱和圆柱的组合体,分别画出它们的三视图组合在一起即可.{@/ts}
{@jx}{@/jx}
{@da}该物体是由一个正六棱柱和一个圆柱组合而成的,正视图反映正六棱柱的三个侧面和圆柱侧面,侧视图反映正六棱柱的两个侧面和圆柱侧面,俯视图是一个正六边形和一个圆(中心重合).它的三视图如图1.2.2-13所示.

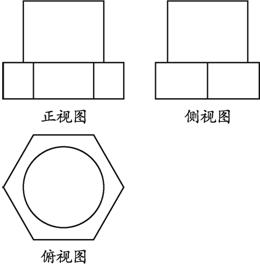
图1.2.2-13
技术感悟：在绘制三视图时,应注意:若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,分界线和可见轮廓线都用实线画出.{@/da}

题型五　由三视图想象几何体
【例5】某简单几何体的三视图如图1.2.2-14所示,那么这个几何体是(　　)

图1.2.2-14
A.三棱锥 
B.四棱锥 
C.四棱台 
D.三棱台
{@ts}由三个视图想象三个方向的外形轮廓,然后综合确定出是什么几何体.{@/ts}
{@jx}

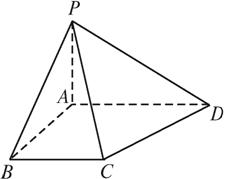
图1.2.2-15{@/jx}
{@da}B
技术感悟：由三视图判断几何体时,不但要分别研究各视图,还要综合考虑几何体的外形轮廓.{@/da}

【例6】一个物体由几块相同的长方体叠成,其三视图如图1.2.2-16所示,试据图回答下列问题:

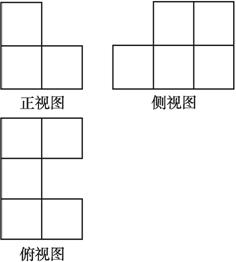
图1.2.2-16
(1)该物体有多少层?
(2)该物体的最高部分位于哪里?
(3)该物体一共由几个小长方体构成?
{@ts}根据三视图的特点,正视图与侧视图都能反映出物体的高(高相等),正视图与俯视图都能反映出物体的长(长相等),俯视图与侧视图都能反映出物体的宽(宽相等).{@/ts}
{@jx}{@/jx}
{@da}(1)该物体一共有两层,从正视图和侧视图都可以看出来;
(2)该物体最高部分位于左侧第一排和第二排;
(3)从侧视图及俯视图可以看出,该物体前后一共三排,第一排左侧2个,右侧1个;第二排左侧2个,右侧没有;第三排左侧1个,右侧1个.该物体一共由7个小长方体组成.
技术感悟：由三视图确定几何体时,要把三个视图两两综合起来,分别考查想象它的长、宽、高,从而正确地得出几何体.{@/da}
 
高考链接
(广东高考)将正三棱柱截去三个角〔如图1.2.2-17(1)所示,A,B,C分别是△GHI三边的中点〕得到几何体如图1.2.2-17(2),则该几何体按图1.2.2-17(2)所示方向的侧视图(或称左视图)为(　　)

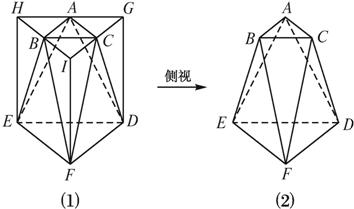
图1.2.2-17
A.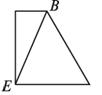
B.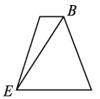
C.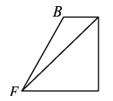
D.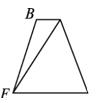
{@ts}观察侧视方向上几何体的外形,根据原棱柱的侧面垂直于底面得几何体中面AED⊥面EFD.从而得侧视图为直角梯形.{@/ts}
{@jx}{@/jx}
{@da}A
技术感悟：考虑几何体的三视图时,可从某些特殊位置入手,一个几何体的三视图就是这个几何体最外围的线面在平面上的射影.{@/da}