细品教材
一、一元二次不等式
我们把含有一个未知数，并且未知数的最高次数是2的不等式ax²+bx+c＞0或ax²+bx+c＜0或ax²+bx+c≥0或ax²+bx+c≤0（a≠0）称为一元二次不等式.元就是未知数，一元就是含有一个未知数.如x²-5x＜0,2x²+6x-10＞0,-3x²+5x+7＜0,5x²＞3,x²-2x-3≤0等都是一元二次不等式.
状元笔记
mx²+2x+6＜0是否为一元二次不等式，取决于m的取值，当m≠0时， mx²+2x+6＜0是一元二次不等式，当m=0时，mx²+2x+6＜0变成2x+6＜0，显然是一元一次不等式.
【示例】甲、乙两种型号的汽车沿同一方向在公路上行驶，其中甲的初速度为0，以加速度为2 m/s²的匀加速方式前进，乙汽车以1 m/s的速度匀速前进，且乙在甲的前方6 m处，那么在多长时间后，甲汽车在乙汽车的前面？
解：假设两汽车行驶的时间为x，则甲汽车的位移为，乙汽车的位移为x＋6，若甲汽车在乙汽车的前面，则满足的不等关系为x²-x-6＞0(x＞0)，解之,得x＞3（x＜-2舍去）.
答:两汽车行使时间超过3秒后，甲汽车在乙汽车的前面.
二、三个二次的联系
一元二次不等式ax²+bx+c＞0（或ax²+bx+c＜0）（a≠0）与一元二次方程ax²+bx+c=0（a≠0）及二次函数y=ax²+bx+c（a≠0）有密切的联系.
如右图所示.

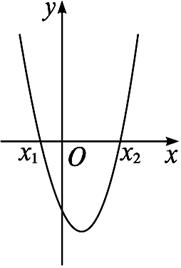
1.如果a＞0,相应的一元二次方程ax²＋bx＋c=0有两个实根x₁，x₂(x₁＜x₂),则二次函数y=ax²+bx+c的图象是开口向上的抛物线，且与x轴交于两点x₁，x₂(x₁＜x₂).由图象容易看出，一元二次不等式ax²+bx+c＞0的解集就是使二次函数y=ax²+bx+c的函数值大于零的取值范围，一元二次方程ax²＋bx＋c=0的两个实根x₁，x₂(x₁＜x₂)就是一元二次不等式ax²+bx+c＞0的解集的两个端点，即为{x|x＞x₂或x＜x₁}.而不等式ax²+bx+c＜0的解集就是使二次函数y=ax²+bx+c的函数值小于零的取值范围，一元二次方程ax²＋bx＋c=0的两个实根x₁，x₂(x₁＜x₂)就是一元二次不等式ax²+bx+c＜0的解集的两个端点,即为{x|x₁＜x＜x₂}.
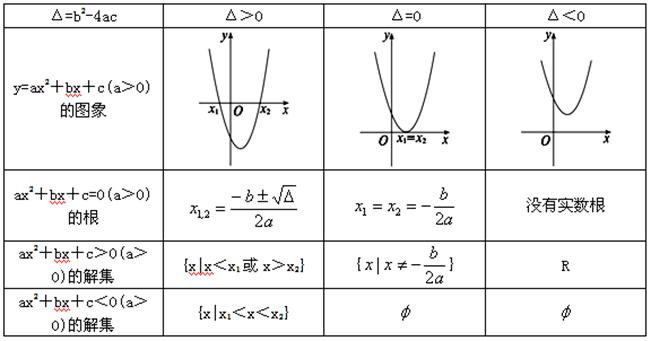
2.如果相应的一元二次方程ax²＋bx＋c=0分别有唯一实根、无实根的话，其相应的二次函数y=ax²＋bx＋c(a＞0)的图象与x轴的位置关系如何？请结合下表加以领会.
一元二次不等式的解集、二次方程的根与二次函数的图象之间的关系.

状元笔记
实际操作中，必须注意二次项的系数的符号,当a＜0时，求解不等式ax²＋bx＋c＞0与ax²＋bx＋c＜0的解集，往往先变形为a＞0时的情况，再求解.
这张表是我们今后求解一元二次不等式的主要工具，必须熟练掌握，其关键是抓住相应的二次函数的图象.当Δ＞0时可用口诀：大于0取两边，小于0取中间.
当a＜0时，能否确定出不等式ax²＋bx＋c＞0与ax²＋bx＋c＜0的解集呢？请类比以上情况的分析，得出答案.
3.通过以上研究，我们可以发现利用图象求解一元二次不等式解集的一般步骤是：
(1)化一元二次不等式为标准形式：ax²+bx+c＞0或ax²+bx+c＜0（a＞0）;
(2)求出一元二次方程ax²+bx+c=0（a＞0）的根,并画出对应函数y=ax²+bx+c（a＞0）的简图；
(3)根据图象写出不等式的解集.
当一元二次不等式为ax²＋bx＋c≥0或ax²＋bx＋c≤0时,要注意解集的端点.
状元笔记
解一元二次不等式主要采用图象法和代数法，通过具体问题的解决过程，要深刻理解不等式ax²＋bx＋c＞0（a≠0）的解集与对应的一元二次方程ax²+bx+c=0的根以及二次函数y=ax²+bx+c的图象之间的关系，明确其解题步骤.对于应用问题，要先确定其中的不等关系，进而用相应的不等式表示出来，再解不等式获得问题的答案.
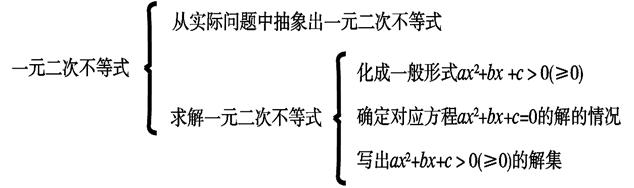
求解一般的一元二次不等式ax²＋bx＋c＞0（a＞0）的解集过程可用如下程序框图表示.

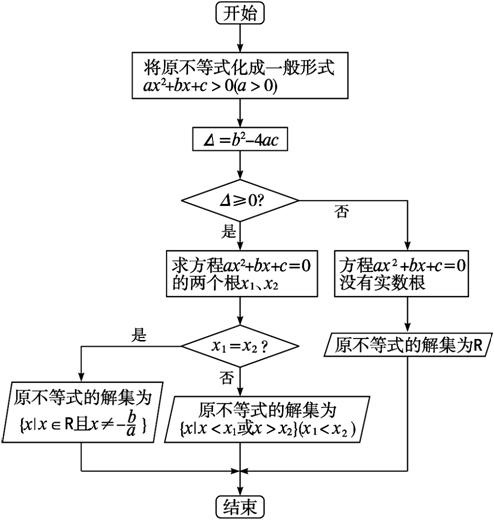
也可以类似地画出ax²＋bx＋c＜0（a＜0）求解的程序框图.根据程序框图可编写求一元二次不等式解集的程序，从而应用计算机来解一元二次不等式.
【示例】解不等式6x-2-3x²＞0.
解析：首先转化为3x²-6x＋2＜0,接着确定方程3x²-6x＋2＝0的解的情况,最后根据二次函数y=3x²-6x+2的图象写出原不等式的解集.
解：原不等式可化为3x²-6x＋2＜0,
因为Δ＞0，
对应方程3x²-6x＋2＝0的解是,
画出相应的二次函数y=3x²-6x+2的图象,如下图所示.

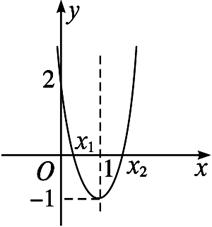
可知原不等式的解集是{}.

基础整理
本节主要内容是一元二次不等式及其解法,为此研究了一元二次不等式的解与二次函数、一元二次方程的联系,逐步体会了形成一元二次不等式有关概念的过程,探究了求解一元二次不等式的解集的方法.首先要从实际问题中建立一元二次不等式ax²+bx+c＞0(≥0),其次确定对应方程ax²+bx+c=0的解,画出对应函数y=ax²+bx+c的图象简图,最后得出不等式的解集.


综合探究
探究课题1含参数一元二次不等式的解法
有些不等式中含有参数,对于形如:ax²+bx+c＞0(≥0)的不等式,首先要讨论二次项系数a是否等于零,如果等于零,那就不是一元二次不等式了;如果二次项系数a小于零,则往往是对原不等式进行转化,变为-ax²-bx-c＜0(≤0),然后再利用求解一般的一元二次不等式的方法加以解决.
另一种情况是一元二次不等式中的一次项或常数项含有参数,这时可能要分类讨论.如:解关于x的不等式x²+(1-a)x-a＞0.由于方程x²+(1-a)x-a=0的解为x₁=-1,x₂=a,需要根据两根的大小关系加以讨论原不等式的解集的情况,即有：
(1)当a＜-1时,原不等式的解集为(-∞,a)∪(-1,+∞);
(2)当a=-1时,原不等式的解集为(-∞,-1)∪(-1,+∞);
(3)当a＞-1时,原不等式的解集为(-∞,-1)∪(a,+∞).
探究课题2高次不等式和分式不等式
(1)高次不等式也是一种很常见的不等式,在许多问题中都牵涉到解高次不等式.另外,许多分式不等式也可以转化为高次不等式,解高次不等式主要使用以下三种方法:
以不等式(x+3)(x-2)(x-4)＞0为例.
方法一：原不等式可化为几个不等式(组)进行求解.
此种方法的本质是分类讨论，强化了“或”与“且”，进一步渗透了“并”与“交”的思想方法.
方法二：不等式（或方程）有三个零点-3，2，4，先在数轴上标出零点，这些零点把数轴分成了若干个区间（如下图）.

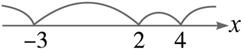
针对这些区间，逐一讨论各因式的符号，情况列表如下：

 
从上表可看出(x+3)(x-2)(x-4)＞0的解集为{x|-3＜x＜2或x＞4}.
方法三：先在数轴上标出零点（如下图）.

根标出来后，不是分区间进行验证讨论，而是直接标出综合因式（x+3）(x-2)(x-4)的正负号,再根据题目要求，直接写出解集为{x|-3＜x＜2或x＞4}.
注：这种方法常称为“数轴标根法”.这种方法的本质是“列表讨论法”的简化及提炼.这样的“线”也可看成是函数y=(x+3)(x-2)(x-4)的图象草图 (y轴未画).利用数轴标根法要先把x的系数化为正数，最好是1，否则很容易写错结论.
(2)简单的分式不等式的解法：

 
通过以上三种形式之一转化为一元一次不等式或一元二次不等式或特殊高次不等式求解.
 
思考发现
1.用一元二次不等式解决实际问题的步骤大致可分为:
(1)理解题意,把条件进行转化,或者画出示意图,理清各量满足的条件;
(2)依据条件建立相应的不等关系,把实际问题抽象为数学问题,即一元二次不等式问题;
(3)解所得的不等式,进而根据题目的实际意义解释原问题.
2.一元一次不等式(组)、一元二次不等式的求解应该很熟练，这是解其他不等式的基础，要充分利用数轴和二次函数的图象，利用数形结合的数学思想可以较为直观地得到不等式的解.
3.对于含有参数的不等式问题，首先想到的应该是分类讨论，要注意分类应不重不漏，最好配合图形进行分类讨论.
4.解不等式的过程实际上就是不断转化的过程,是同解不等式的逐步代换,基本思路是:代数化、分式整式化、有理化、低次化、低维化，最后转化到可解的常见一元一次不等式、一元二次不等式上来.