典例精析
一、基础知识题型
【例1】如图10.2-3是1998年参加国际教育评估的15个国家学生的数学平均成绩的统计图,则平均成绩大于或等于60的国家个数是(　　)

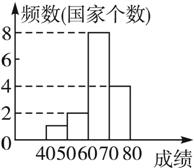
图10.2-3
A.4
B.8
C.10
D.12
{@jx}由频数直方图可知,平均成绩为60~70的有8个国家,70~80的有4个国家,则平均成绩大于或等于60的国家个数有8+4=12个.{@/jx}
{@da}D
技术化提示
准确读图是解决相关统计问题的关键.{@/da}

【例2】如图10.2-4是某班全体学生外出时乘车、步行、骑车的人数分布直方图和扇形分布图(两图都不完整)，则下列结论中错误的是(　　)

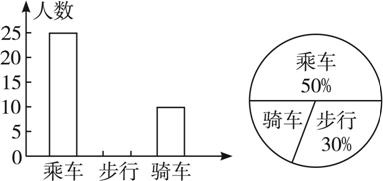
图10.2-4
A.该班总人数为50人
B.骑车人数占总人数的20%
C.步行人数为30人
D.乘车人数是骑车人数的2.5倍
{@jx}由直方图可知，乘车人数为25人，骑车人数为10人，由扇形统计图可知，乘车人数占全班总人数的50%，步行人数占全班人数的30%，所以该班总人数为25÷50%=50(人)，步行人数为50×30%=15(人).{@/jx}
{@da}C
技术化提示
要充分挖掘每一个统计图所反映的信息,通过综合、计算从而解决相关问题.{@/da}

【例3】为了了解中学生的身体发育情况,对某中学同龄的60名女学生的身高进行了测量,结果如下:(单位:厘米):
167　154　159　166　169　159　156　166　162　158
159　156　166　160　164　160　157　156　157　161
158　158　153　158　164　158　163　158　153　157
162　162　159　154　165　166　157　151　146　151
158　160　165　158　163　163　162　161　154　165
162　162　159　157　159　149　164　168　159　153
请画出频数分布直方图.
{@jx}首先观察这组数据,找出最大值为169,最小值为146,它们的差是169-146=23(厘米),说明身高(x)的变化范围是23厘米,因此可以把数据按身高的范围进行分组,取组距为3厘米,则可以把数据按范围146≤x＜149,149≤x＜152,152≤x＜155,155≤x＜158,158≤x＜161,161≤x＜164,164≤x＜167,167≤x＜170,分成8个组,从而整理出频数分布表.{@/jx}
{@da}最大值与最小值的差为169-146=23(厘米).
若组距为3厘米,则,所以应该分为8组.
整理得频数分布表如下.

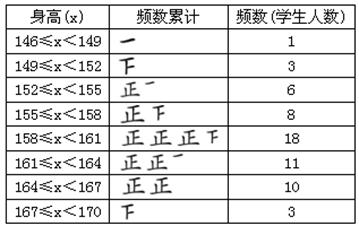
根据频数分布表画出频数分布直方图(如图10.2-5).

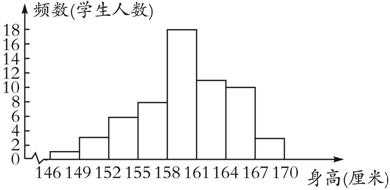
图10.2-5
技术化提示
频数分布直方图中的组距与组数的确定是一个难点,它不仅与数据的多少有关,还与数据本身的特点有关.如果组数太多,数据的分布会过于分散;而组数太少,数据的分布会过于集中,这都不便于观察数据分布的特征和规律.{@/da}

二、综合拓展题型
【例4】图10.2-6是某单位职工的年龄(取正整数)的频数分布直方图，根据图形提供的信息回答下列问题：

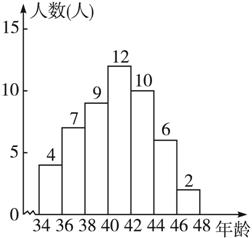
图10.2-6
(1)本单位在哪个年龄段的人数最多?哪个年龄段的人数最少?各是多少?
(2)36~38岁的职工有多少人?
(3)该单位职工共有多少人？
(4)不小于38岁但小于42岁的职工人数占职工总人数的百分比是多少？
{@jx}结合直方图的特点,读懂图形,获取有用信息.{@/jx}
{@da}(1)本单位职工在40~42岁这个年龄段的人数最多,是12人;46~48岁这个年龄段的职工人数最少,是2人.
(2)36~38岁的职工有7人.
(3)本单位职工共有4+7+9+12+10+6+2= 50(人).
(4)不小于38岁但小于42岁的职工人数为9+12=21,
所占总数的百分比为.
技术化提示
利用直方图中的信息计算时,注意不能遗漏,不能重复.{@/da}

三、探究创新题型
【例5】某班48名学生，在一次英语测试中，分数只取整数，为了统计成绩，绘制出频数分布直方图，如图10.2-7.从左到右的小矩形的高度比是1∶3∶6∶4∶2，则分数在70.5到80.5之间的人数是多少？

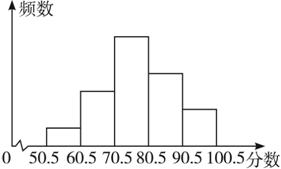
图10.2-7
{@jx}错解：由题意可知分数在70.5到80.5之间的人数最多，再由直方图可知分数在70.5到80.5之间的人数是6.
错解分析：因为频数分布直方图各小长方形的高是该小组的频数，各小矩形的高度比是1∶3∶6∶4∶2，并不是各小组的频数，而是告诉我们各小组的频数之比.{@/jx}
{@da}正解：设第一小组的频数为a，则其他小组的频数为3a、6a、4a、2a，由题意得a+3a+6a+4a+2a=48.解得a=3.所以6a=18.所以分数在70.5到80.5之间的人数是18.{@/da}

【例6】某中学举行了一次演讲比赛，分段统计参赛同学的成绩，结果如下表(分数均为整数，满分为100分)：

请根据表中提供的信息，解答下列问题：
(1)参加这次演讲的同学共有_______人.
(2)已知成绩在91~100分的同学为优胜者,那么优胜率是_______.
(3)所有参赛同学的平均得分M(分)在什么范围内?
答:________________________________.
(4)将成绩频数分布直方图(图10.2-8)补充完整.

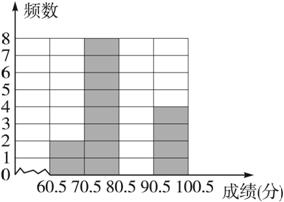
图10.2-8
{@jx}由统计图表易得参赛人数为2+8+6+4=20,优胜率,平均得分M的范围,可以从两个端点取值计算,全取最低值,得到最低分,全取最高值,得最高分,即最低分是,
最高分为,所以77≤M≤86.{@/jx}
{@da}(1)20
(2)20%
(3)77≤M≤86
(4)如图10.2-9所示.

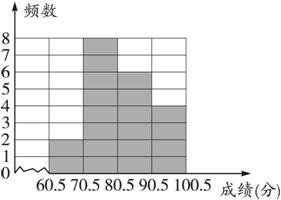
图10.2-9
技术化提示
在利用统计图表解决实际问题时,要明确各种统计图的特点,正确理解统计图表的意义.{@/da}

链接中考
本节知识在实际生活中应用性强,它是中考的热点内容,题型有选择题、填空题,有时也有解答题,考分3~6分,以考查频数、频率、频数分布表、频数分布直方图等内容为主,重点考查学生读图、识图、利用图形获取信息的能力.具体考查方向归纳如下:
一是考查收集整理数据，绘制频数分布直方图.
二是考查读图的基本能力.也就是给一个频数分布直方图，让你通过读图，观察得出相关信息，回答相关统计问题.
三是考查用频数分布直方图解决相关综合应用问题.如给一个统计表，而统计表只有一部分数据，要求由此表推算出待求的数据；或给一个不完整的频数分布直方图，要求根据已知条件，补全频数分布直方图等等.
【例1】(温州)九年级(1)班共50名同学,图10.2-10是该班体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于29分的成绩评为优秀,则该班此次成绩优秀的同学人数占全班人数的百分比是(　　).
九年级(1)班50名同学体育模拟测试成绩频数分布直方图

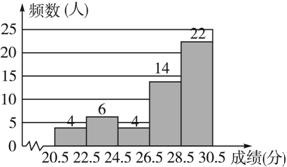
图10.2-10
A.20%
B.44%
C.58%
D.72%
{@da}B{@/da}
{@jx}由频数分布直方图可知,不低于29分的共有22名学生,占全班人数的百分比为.{@/jx}

【例2】(福州)如图10.2-11的统计图描述了九年级(1)班学生在为期一个月的读书月活动中,三个阶段(上旬、中旬、下旬)日人均阅读时间的情况.
(1)从统计图可知,九年级(1)班共有学生_______人;
(2)图①中a的值是_______;
(3)从图①②中判断，在这次读书月活动中，该班学生每日阅读时间_______(填“普遍增加了”或“普遍减少了”)；
(4)通过这次读书月活动，如果该班学生初步形成了良好的每日阅读习惯，参照以上统计图的变化趋势，至读书月活动结束时，该班学生日人均阅读时间在0.5~1小时的人数比活动开展初期增加了_______人.
活动上旬频数分布直方图

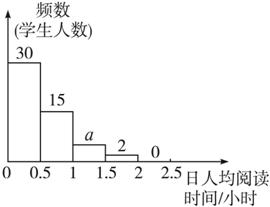
①
活动中旬频数折线图

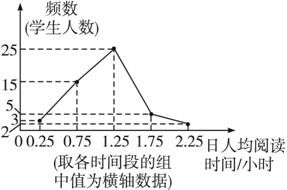
②
活动下旬频数分布扇形图

③
图10.2-11
{@da}(1)50　(2)3　(3)普遍增加了　(4)15{@/da}
{@jx}此题将频数分布直方图、频数折线图、频数分布扇形图放在一起,要善于挖掘它们所反映的信息之间的联系，综合起来,从而解决相关问题.{@/jx}