典例精析
一、基础知识题型
【例1】如图23.1-4,以点O为旋转中心,将∠1按顺时针方向旋转110°,得到∠2.若∠1=40°,则∠2=__________度.
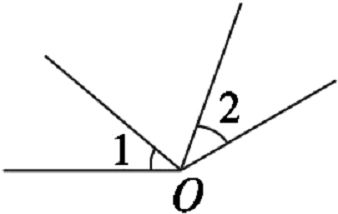
图23.1-4
{@jx}根据图形在旋转过程中大小不变的性质,可求∠2的度数.{@/jx}
{@da}40
技术化提示:在求解图形旋转后相关线段或角度时,关键要抓住图形在旋转过程中大小不变的性质.{@/da}
【例2】图23.1-5可以看作是一个等腰直角三角形旋转若干次而生成的,则每次旋转的最小角度是________.
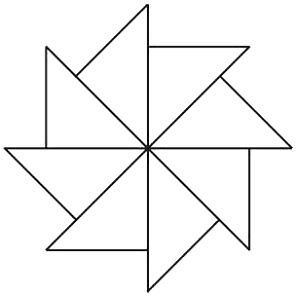
图23.1-5
{@jx}从图中可以看出,这个图形共由八个小的等腰直角三角形所形成,所以可知旋转的最小角度应为一个周角360°的 .{@/jx}
.{@/jx}
{@da}45°
技术化提示:像这种由一个图形通过某种旋转得到的图案,要挖掘整体与部分的内在联系.{@/da}
【例3】正方形ABCD在坐标系中的位置如图23.1-6(1)所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )
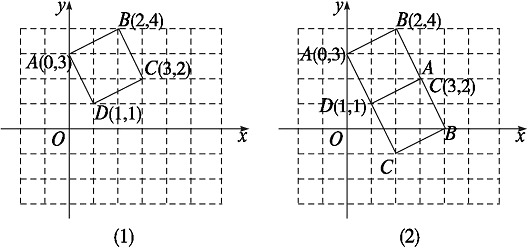
图23.1-6
A.(-2,2)
B.(4,1)
C.(3,1)
D.(4,0)
{@jx}在直角坐标系内将正方形ABCD绕D点顺时针旋转90°后,可知点B在x轴的正半轴上,由此可得这个点的坐标.{@/jx}
{@da}D
技术化提示:求一个图形旋转后的图形的某点的坐标,要注意把握三点:一是图形旋转变换的性质;二是图形的全等关系;三是点所在象限的符号.{@/da}
【例4】如图23.1-7,在正方形ABCD中,E在BC上,∠FDE=45°,△DEC按顺时针旋转一个角度后,到达△DGA的位置.
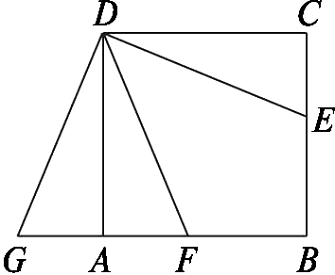
图23.1-7
(1)指出图中的旋转中心,并说明旋转角度是多少?
(2)指出旋转图形的对应线段和对应角.
{@jx}错解:(1)∵△DEC绕点D按顺时针旋转90°后,到达△DGA的位置,∴旋转中心是点D,旋转角度是90°.
(2)对应线段分别是:DC与DA,DE与DF,CE与AF;对应角分别是:∠CDE与∠ADF,∠C与∠DAF,∠DEC与∠DFA.
错解分析:(2)把与△DEC全等的△DFA,错看成是△DEC按顺时针方向旋转一个角度后得到的三角形,导致所得的对应线段和对应角出现错误.{@/jx}
{@da}正解:(1)同上.
(2)对应线段分别是:DE与DG,DC与DA,CE与AG;对应角分别是:∠CDE与∠ADG,∠C与∠DAG,∠DEC与∠G.
技术化提示:在判断旋转图形的对应线段和对应角时,先要从整体上抓住旋转后的图形,再从对应关系上确定对应线段和对应角.{@/da}
【例5】如图23.1-8,在正方形网格中,以点A为旋转中心,将△ABC按逆时针方向旋转90°,画出旋转后的△AB1C1.
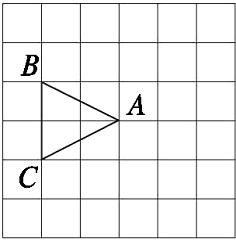
图23.1-8
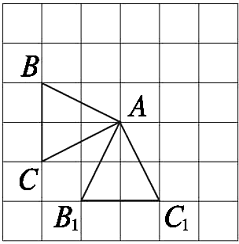
图23.1-9
{@jx}由于旋转前后的两个三角形是共顶点的,所以在正方形网格中,只需将AB边和AC边分别绕点A按逆时针方向旋转90°,再连接另两个端点,就可得所求的△AB1C1.{@/jx}
{@da}如图23.1-9所示,将线段AB、AC按逆时针方向分别旋转90°,设它们旋转后分别与正方形“网格点”相交于B1、C1,连接B1、C1.
则△AB1C1就是△ABC绕点A按逆时针方向旋转90°后所得的三角形.
技术化提示:在正方形网格中旋转图形,所旋转的图形一般是网格图形,即图形上的各个点都在网格的交点上,因此,根据旋转作图的基本方法可以很容易地画出旋转后的图形.{@/da}
二、综合拓展题型
【例6】如图23.1-10,作出△ABC绕点O旋转45°后的三角形.
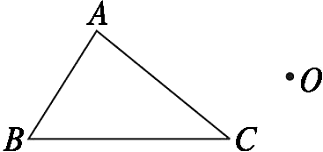
图23.1-10
{@jx}由于题中没有说明旋转方向,这样顺时针旋转可以,逆时针旋转也可以,所以有两种作法.根据旋转特征和题设旋转中心与旋转角度,先画出已知图形中的顶点的对应点,然后连接相关线段,便可得所作图形.
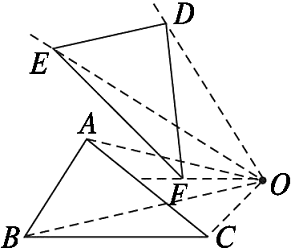
图23.1-11{@/jx}
{@da}解法一:(1)如图23.1-11所示,连接OA、OB、OC;
(2)分别以OA、OB、OC为一边,按顺时针方向作∠AOD、∠BOE、∠COF,使∠AOD=∠BOE=∠COF=45°;
(3)分别在射线OD、OE、OF上截取OD=OA,OE=OB,OF=OC;
(4)连接DE、EF、FD,则△DEF就是△ABC绕点O按顺时针方向旋转45°后所得的三角形.
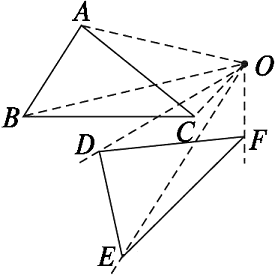
图23.1-12
解法二:(1)如图23.1-12所示,连接OA、OB、OC;
(2)分别以OA、OB、OC为一边,按逆时针方向作∠AOD、∠BOE、∠COF,使∠AOD=∠BOE=∠COF=45°;
(3)分别在射线OD、OE、OF上截取OD=OA,OE=OB,OF=OC;
(4)连接DE、EF、FD,则△DEF就是△ABC绕点O按逆时针方向旋转45°后所得的三角形.
技术化提示:利用旋转的性质作图时,要注意抓住三点:一是旋转角度;二是旋转方向;三是旋转中心到旋转前后两个图形的对应点的距离.{@/da}
【例7】如图23.1-13,在直角坐标系中,Rt△AOB的两条直角边OA,OB分别在x轴的负半轴,y轴的负半轴上,且OA=2,OB=1,将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.
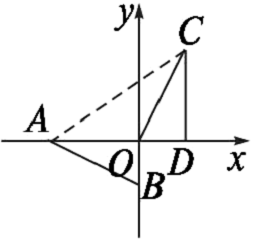
图23.1-13
(1)写出点A,C的坐标;
(2)求点A和点C之间的距离.
{@jx}(1)根据图形旋转的性质可得AO=CD,OB=OD,由此可得A,C的坐标;(2)在Rt△ACD中,利用勾股定理可求解.{@/jx}
{@da}(1)由题意,得AO=CD,OB=OD.
∵OA=2,OB=1,
∴点A的坐标是(-2,0),点C的坐标是(1,2).
(2)如图23.1-13,连接AC.在Rt△ACD中,AD=OA+OD=3,CD=2,
∴AC2=CD2+AD2=22+32=13.
∴AC= .
.
技术化提示:(1)先根据图形旋转的性质得对应边相等,后结合点在各象限的符号求解;(2)利用勾股定理求解.{@/da}
三、探究创新题型
【例8】 如图23.1-14(1),已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.
(1)求证:BP=DP;
(2)如图23.1-14(2),若四边形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若有,请给予证明;若没有,请用反例加以说明.
(3)试选取正方形ABCD的两个顶点,分别与四边形PECF的两个顶点连接,使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中,长度始终相等,并证明你的结论.
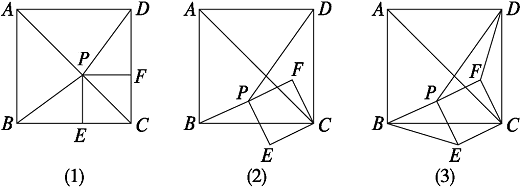
图23.1-14
{@jx}(1)利用正方形的性质和三角形全等可得;(2)四边形PECF绕点C按逆时针方向旋转的过程中,点P逐渐靠近BC,当P点落在BC边上时,显然DP>BP;(3)由图上观察可知,当大正方形的一边与小正方形的一边组成的两个三角形夹角相等时,就存在两条线段相等.{@/jx}
{@da}(1)如图(1),在△ABP与△ADP中,AB=AD,∠BAP=∠DAP,AP=AP,
∴△ABP≌△ADP,∴BP=DP.
(2)不是总成立.当四边形PECF绕点C按逆时针方向旋转,点P旋转到BC边上时,DP>DC>BP,此时BP=DP不成立.
(3)如图(3),连接BE、DF,则BE与DF始终相等.
证明:由图(1),可证四边形PECF为正方形.
∴∠ECF=∠BCD=90°.
∴∠BCE+∠BCF=∠DCF+∠BCF.
∴∠BCE=∠DCF.
在△BEC与△DFC中,∵BC=DC,∠BCE=∠DCF,CE=CF,
∴△BEC≌△DFC.∴BE=DF.
技术化提示:像这类图形旋转运动,要注意从两个方面探究:一方面是从特殊中发现其一般规律;另一方面是从变化中发现其不变的性质.{@/da}
链接中考
图形的旋转是近几年中考的新内容,考查的形式多样,既有选择题和填空题,也有解答题.其考查内容包括下列几个方面:一是对图形旋转概念的理解;二是运用图形旋转的性质计算相关问题;三是进行简单的旋转作图.分值约为3~6分.
【例1】 (2008・江苏无锡,16)如图23.1-15,△OAB绕点O逆时针旋转80°到△OCD的位置,已知∠AOB=45°,则∠AOD等于( )
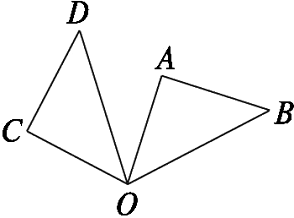
图23.1-15
A.55°
B.45°
C.40°
D.35°
{@da}D{@/da}
{@jx}∠AOD=∠BOD-∠AOB=80°-45°=35°.{@/jx}
【例2】(2008・辽宁大连,15)如图23.1-16(1),画出△OAB绕O点按逆时针方向旋转90°时的△OA′B′.
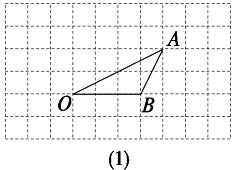
图23.1-16
{@da}△OA′B′如图23.1-16(2)所示.
 {@/da}
{@/da}
{@jx}按照旋转作图的基本步骤可作.{@/jx}
【例3】 (2007・广东中山,20)已知等边△OAB的边长为a,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2.
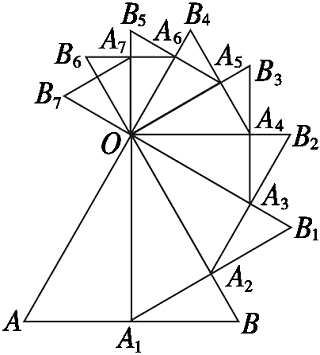
图23.1-17
(1)求线段OA2的长;
(2)若再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,△OAnBn(如图23.117).求△OA6B6的周长.
{@da}(1)OA2= OA1=
OA1= ×(
×( OA)=
OA)= OA=
OA= a.
a.
(2)依题意OA1= OA,OA2=
OA,OA2= OA1=(
OA1=( )2OA,OA3=
)2OA,OA3= OA2=(
OA2=( )3OA.
)3OA.
依次类推,OA6=( )6OA=
)6OA= OA=
OA= a.
a.
∴△OA6B6的周长=3OA6= a.{@/da}
a.{@/da}
{@jx}利用等边三角形底边高线的性质,将问题转化为求特殊直角三角形(60°角)的直角边.{@/jx}

 .{@/jx}
.{@/jx}







 .
.


 {@/da}
{@/da}
 OA1=
OA1= ×(
×( OA)=
OA)= OA=
OA= a.
a. OA,OA2=
OA,OA2= OA1=(
OA1=( )2OA,OA3=
)2OA,OA3= OA2=(
OA2=( )3OA.
)3OA. )6OA=
)6OA= OA=
OA= a.
a. a.{@/da}
a.{@/da}